Featured image of post 二分图最大匹配匈牙利算法
算法

二分图最大匹配匈牙利算法

二分图最大匹配

前言：其实老早就学了，但是之前学的时候不透彻，稀里糊涂背背模板就过去了。果然，在最近一次原题检测上找到了我，然后就“暴毙”了。
我就意识到学算法不能这么学，要摸清楚规律、掌握证明方法、思考推论过程。
俗话说“温故而知新”，的确，我也在复习的过程中有了更透彻的理解。所以我决定写一篇笔记。
本文有很多地方直接搬用了一些参考资料，所以本篇笔记原创部分主要为对关键部分进行解释。

建议：草稿纸和笔永远是最好的工具。在看本文过程中，要仔细思考任何一部分，不要囫囵吞枣。

注：本篇文章是我这个小蒟蒻写的，真正的dalao请看个玩笑便好，不必争论对错（但是欢迎指出文章存在的小错误）。

二分图初步

建议：如果你已对此有些许了解，可以根据目录直接跳到二分图匹配部分

什么是二分图

参考资料是这样介绍的：

  • 二分图又称作二部图，是图论中的一种特殊模型。
  • 设 $G=(V, E)$ 是一个无向图。如果顶点集 $V$ 可分割为两个互不相交的子集 $X$ 和 $Y$，并且图中每条边连接的两个顶点一个在 $X$ 中，另一个在 $Y$ 中，则称图 $G$ 为二分图。

但其实可以简化成一张图去理解：

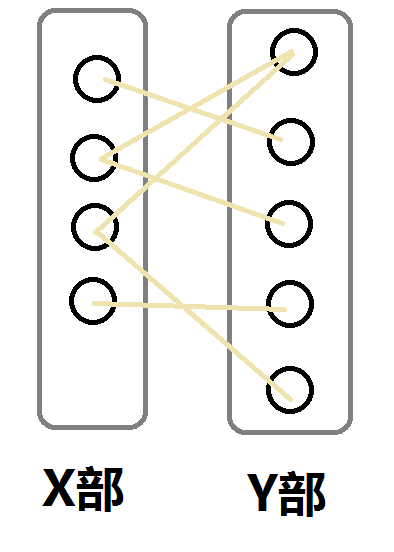
上图就是一个二分图。

二分图性质

参考资料：

  • 定理：当且仅当无向图 $G$ 的每一个回路的边数均是偶数时，$G$ 才是一个二分图。如果无回路，相当于任一回路的边数为 $0$，故也视为二分图。

二分图判定

参考资料这里写得太复杂了，简单的话描述一下：

  • 如果是一个连通图
    1. 从顶点 $1$ 开始宽度遍历整个图（$BFS$）
    2. 对遍历到的点进行染色，只染黑、白两色
    3. 染色过程中做到相邻点的颜色不同
  • 如果不是一个连通图
    • 在每个连通块中作判定，判定方法与上面相似

如下图，可判定为一个二分图：

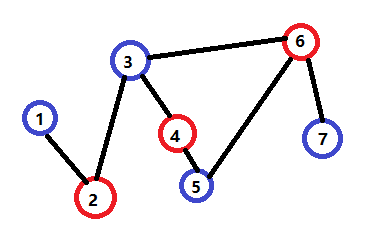
为了观察方便，这里用红、蓝两色代替了黑、白两色。

二分图匹配

什么是匹配

先看看参考资料怎么说：

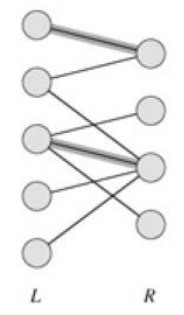
给定一个二分图 $G$，在 $G$ 的一个子图 $M$ 中，$M$ 的边集 ${E}$ 中的任意两条边都不依附于同一个顶点，则称 $M$ 是一个匹配。

图中加粗的边是数量为 $2$ 的匹配。

这里讲得很清楚，不过多赘述（下文当资料讲得很简单明了时，也不会再过多解释）。

什么是最大匹配

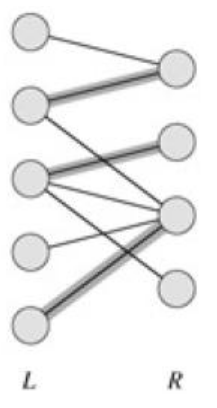
选择边数最大的子图称为图的最大匹配问题。
如图加粗的边是一个最大匹配：

可以简单理解为使 $X$ 部的顶点和 $Y$ 部的顶点匹配尽可能多。

什么是增广路径

设 $M$ 为二分图 $G$ 已匹配边的集合，若 $P$ 是图 $G$ 中一条连通两个未匹配顶点的路径（$P$ 的起点在 $X$ 部，终点在 $Y$ 部，反之亦可），并且属 $M$ 的边和不属 $M$ 的边(即已匹配和待匹配的边)在 $P$ 上交替出现，则称 $P$ 为相对于 $M$ 的一条增广路径。

增广路径是一条“交错轨”。也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有……最后一条边没有参与匹配,并且起点和终点还没有被选择过，这样交错进行，显然 $P$ 有奇数条边。

为什么 $P$ 会有奇数条边呢？

根据定义，$P$ 路径的起点和终点不在同一个部，所以必然是奇数条边。

下面来根据这个图找一下增广路：

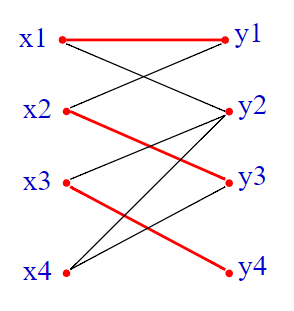
易得一条路径：

$$ x_4 \rightarrow y_3 \rightarrow x_2 \rightarrow y_1\rightarrow x_1\rightarrow y_2 $$

因为 $y_2$ 是 $Y$ 部中未匹配的点，所以此路径是增广路径。

其中 $\in M$ 的边有 $(x_2,y_3),(x_1,y_1)$，不属于匹配的边有 $(x_4,y_3),(x_2,y_1),(x_1,y_2)$。
可见不属于匹配的边要多一条。

如果我们想让情况变成匹配边会多一条，那就思考一下“取反”操作，即将匹配边变为非匹配边，反之同理。
可得：

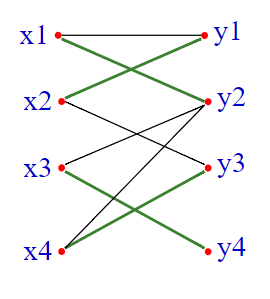
可以得到这样的匹配 $M’=((x_3,y_4),(x_4,y_3),(x_2,y_1),(x_1,y_2))$。

仔细思考，发现匹配仍然合法。交错轨也还存在。
可以证明，当不能再找到增广路时，就已经得到了一个最大匹配。

为什么？
假设还能再找到一条增广路，那经过取反操作必定可以多增加一条匹配边。那最大匹配是最终形态，必定不会再有一条增广路。

而这，就是匈牙利算法的思路。

增广路径性质

  • $P$ 的路径长度必定为奇数，第一条边和最后一条边都不属于 $M$，因为两个端点分属两个集合，且未匹配。
  • $P$ 经过取反操作可以得到一个更大的匹配 $M’$。
  • $M$ 为 $G$ 的最大匹配当且仅当不存在相对于 $M$ 的增广路径。

以上很好理解，根据定义可推出。

匈牙利算法

为什么要用匈牙利算法

匈牙利算法就是用增广路求最大匹配问题，由匈牙利数学家 Edmonds 于1965年提出。

匈牙利算法长什么样

  1. 置 $M$ 为空
  2. 找出一条增广路径 $P$，通过取反操作获得更大的匹配$M’$代替$M$
  3. 重复步骤2，直至再也找不出新增广路

怎么找增广路

第一个想法肯定是用 dfs：
从 $X$ 部一个未匹配的顶点 $u$ 开始，找一个未访问的邻接点 $v$（$v$ 一定是 $Y$ 部顶点）。
对于 $v$，分两种情况：

  • 如果 $v$ 未匹配，则已找到一条增广路。
  • 如果 $v$ 已匹配，设 $v$ 的匹配顶点为 $w$（$w$ 一定属 $X$ 部）。此时边 $(w,v)$ 为匹配边，根据“取反”思想，要将 $(w,v)$ 改为未匹配，$(u,v)$ 改为匹配。怎样才能实现这一点？要看从 $w$ 为起点出发能不能找到一条新增广路 $P’$。如果成功，那 $u\rightarrow v\rightarrow P’$ 就是以 $u$ 为起点的增广路径。

那么我们就成功地把匈牙利算法核心部分搞懂了，可以上代码了。

代码实现匈牙利算法

寻找增广路部分

code：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// cx[i]表示与X部i点匹配的Y部顶点编号，cy[i]表示与Y部i点匹配的X部顶点编号
bool dfs(ll x)
{
    for (auto y : v[x])
    {
        if (!vis[y])
        {
            vis[y] = 1;
            if (cy[y] == -1 || dfs(cy[y]))
            {
                cx[x] = y, cy[y] = x;
                return 1;
            }
        }
    }
    return 0;
}

匈牙利算法主函数

code：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

#define mem(a,b) memset(a,b,sizeof(a))
ll maxmatch()
{
    ll ans = 0;
    mem(cx, -1);
    mem(cy, -1);

    rp(i, 1, n)
    {
        if (cx[i] == -1)
        {
            mem(vis, 0);
            ans += dfs(i);
        }
    }
    return ans;
}

板题&后记

前几天原题检测，考了一些最大匹配的原题。复习时才发现有很多纰漏平时没注意到，所以写了这篇文章。

还是挺耗费精力的，因为这种知识和图片打交道比较多，制作图片和上传都挺麻烦的。

挂个板子吧。

[USACO4.2]完美的牛栏The Perfect Stall

这里挂两个代码，在连接$X$部与$Y$部方面有些不同，根据个人习惯取舍咯……
本人主要是按照题目意思及时变通，并没有什么常用的版本。

版本 1：用一个数组存下两种关系（个人较常用）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define rp(i, o, p) for (ll i = o; i <= p; ++i)
#define pr(i, o, p) for (ll i = o; i >= p; --i)
#define mem(a, b) memset(a, b, sizeof(a))

const ll MAXN = 1e4 + 5; // 这里要注意一下，不然会RE

ll n, m;
ll s[MAXN];
bool vis[MAXN];
ll c[MAXN];
ll sum, en[MAXN << 1], hed[MAXN], lst[MAXN << 1];

void add(ll x, ll y) {
    en[++sum] = y;
    lst[sum] = hed[x];
    hed[x] = sum;
}

bool dfs(ll x) {
    for (ll i = hed[x]; i; i = lst[i]) {
        ll y = en[i];
        if (!vis[y]) {
            vis[y] = 1;
            if (!c[y] || dfs(c[y])) {
                c[y] = x;
                return 1;
            }
        }
    }
    return 0;
}

ll maxmatch() {
    ll ans = 0;
    rp(i, 1, n) {
        mem(vis, 0);
        if (dfs(i))
            ++ans;
    }
    return ans;
}

int main() {
    scanf("%lld%lld", &n, &m);
    rp(i, 1, n) {
        scanf("%lld", &s[i]);
        rp(j, 1, s[i]) {
            ll t;
            scanf("%lld", &t);
            add(i, t);
        }
    }
    printf("%lld\n", maxmatch());
    return 0;
}

版本 2：不同部用不同数组（根据题目不同偶尔采用）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define rp(i, o, p) for (ll i = o; i <= p; ++i)
#define pr(i, o, p) for (ll i = o; i >= p; --i)
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a))

const ll MAXN = 200 + 5;

ll n, m;
vector<ll> v[MAXN << 1];
ll cx[MAXN], cy[MAXN << 1];
bool vis[MAXN << 1];

bool dfs(ll x) {
    for (auto y : v[x]) {
        if (!vis[y]) {
            vis[y] = 1;
            if (cy[y] == -1 || dfs(cy[y])) {
                cx[x] = y, cy[y] = x;
                return 1;
            }
        }
    }
    return 0;
}

ll maxmatch() {
    ll ans = 0;
    mem(cx, -1);
    mem(cy, -1);

    rp(i, 1, n) {
        if (cx[i] == -1) {
            mem(vis, 0);
            ans += dfs(i);
        }
    }
    return ans;
}

int main() {
    scanf("%lld%lld", &n, &m);
    rp(i, 1, n) {
        ll x;
        scanf("%lld", &x);
        rp(j, 1, x) {
            ll y;
            scanf("%lld", &y);
            v[i].pb(y + n), v[y + n].pb(i);
        }
    }

    printf("%lld\n", maxmatch());

    return 0;
}