凸透镜成像原理

前言

凸透镜成像原理是个有意思的知识。初二教科书会以实验的方式告诉我们原理。

快要参加中考了，复习的时候老师说了一条公式：

但它为什么是对的，所以来证明一下。

几何法

要点：三角形相似。

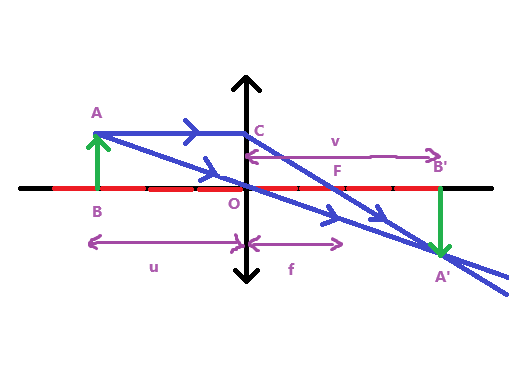
证明

$证：$

$\because\triangle ABO\triangle A’B’O$ $\qquad$ (三角形ABO相似于三角形A’B’O)

$\therefore AB:A’B’=u:v$

$\because\triangle COF∽\triangle A’B’F$

$\therefore CO:A’B’=f:(v-f)$

$\because 四边形ABOC为矩形$

$\therefore AB=CO$

$\therefore AB:A’B’=f:(v-f)$ $\therefore u:v=f:(v-f)$

$\therefore u(v-f)=vf$

$\therefore uv-uf=vf$

$\because uvf\neq 0$

$\therefore \frac{uv}{uvf}-\frac{uf}{uvf}=\frac{vf}{uvf}$

$\therefore \frac{1}{f}-\frac{1}{v}=\frac{1}{u}$

$即$

$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$

$证毕$.

函数法

要点：一次函数，正比例函数。

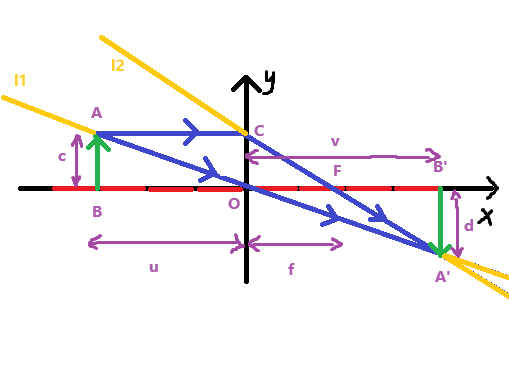
证明

步骤

　　（一）为便于用函数法解决此问题，将凸透镜的主光轴与平面直角坐标系的横坐标轴（$x$ 轴）关联（即重合），将凸透镜的理想折射面与纵坐标轴（$y$ 轴）关联，将凸透镜的光心与坐标原点关联.则：点 $A$ 的坐标为 $(-u,c)$，点 $F$ 的坐标为 $(f,0)$，点 $A’$ 的坐标为 $(v,-d)$，点 $C$ 的坐标为 $(0,c)$.

　　（二）将 $AA’$，$A’C$ 双向延长为直线 $l_1$,$l_2$，视作两条函数图象.由图象可知：直线 $l_1$ 为正比例函数图象，直线 $l_2$ 为一次函数图象.

　　（三）设直线 $l_1$ 的解析式为 $y=k_1x$，直线 $l_2$ 的解析式为 $y=k_2x+b$.

依题意，将 $A(-u,c)$，$C(0,c)$，$F(f,0)$ 代入相应解析式，得

得

$\therefore 两函数解析式为$

$\therefore 两函数交点 A’(x,y) 满足方程组$

$\because A’(v,-d)$

$\therefore -\frac{c}{u}v=-\frac{c}{f}v+c=-d$

$\therefore \frac{c}{u}v=\frac{c}{f}v+c=d$

$\therefore \frac{cv}{u}=\frac{cv}{f}+c$

$\therefore cvf=cuv-cuf$（两边同乘 $uf$）

$\therefore vf=uv-uf$

$\because uvf\neq0$

$\therefore \frac{vf}{uvf}=\frac{uv}{uvf}-\frac{uf}{uvf}$

$\therefore \frac{1}{u}=\frac{1}{f}-\frac{1}{v}$

$即$

$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$

$证毕.$

结尾

这篇文章之前写过了，2024.6.6 进行了修改，使其更加可读。