Featured image of post 平衡树详解
算法

平衡树详解

平衡树

是一种二叉查找树，其平衡性使得树的深度在$\log n$以内，增加、删除等操作可以做到 $O(\log n)$.

平衡树的实现有多种，本文主要介绍 AVL，Treap，FHQ Treap 与 Splay .

AVL

介绍

AVL 是这些算法中时间复杂度最优秀的，也是码量最大的.

其原因在于：AVL 是维护绝对平衡，即左子树高度与右子树高度之差 $\leq 1$

所以每一次维护造就了优秀的时间复杂度 与超大的码量 .

平衡维护

可以说，平衡维护是铸造二叉平衡树最关键的一步，也是最难理解的一步.

如何维护？

1.先判断左子树与右子树高度之差.
2.再判断较高的那一棵子树是它的左子树高还是右子树高.
3.最后再进行旋转操作使其平衡.

相信第1步很容易理解，这里不作过多解释.

为什么会有第2步的判断？

因为可能出现不同的情况，我们也需要做出不同的旋转.

如下图，左子树根节点（节点3）的左儿子（节点2）使左子树高度增加为2，而右子树高度为0，所以平衡树不平衡.
1
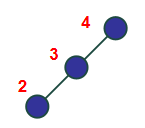
再如下图，左子树根节点（节点15）的右儿子（节点18）使左子树高度增加为2，而右子树高度为0，所以平衡树不平衡.
2

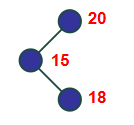
同理，也有右子树高度高于左子树的情况.
3
4

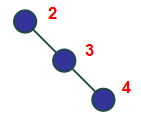
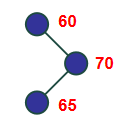
明显可见，当多出来的那个节点与它的父亲、父亲的父亲（祖父）成一条线时，只需要通过一次旋转.
当不成一条线时，需要通过两次旋转.

单旋转分为两种，左旋（zag）与右旋（zig）.

如下图，为左旋.
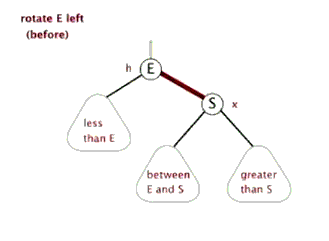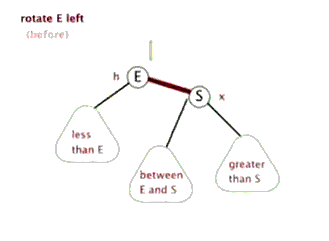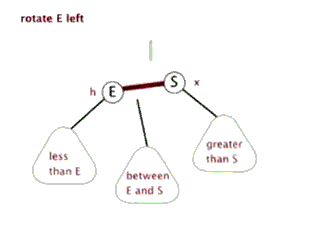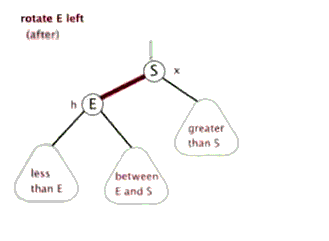
left rotate
如下图，为右旋.
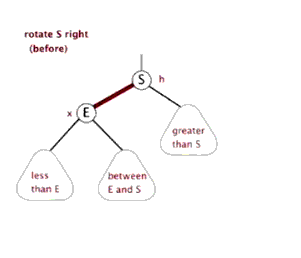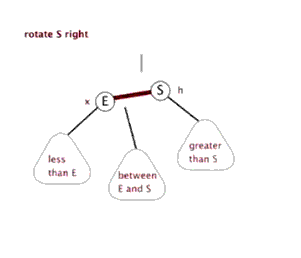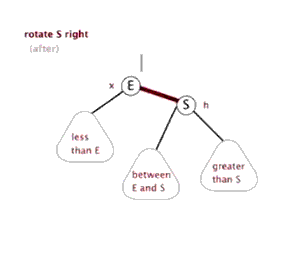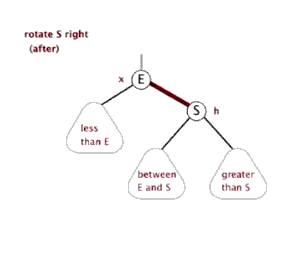
right rotate

双旋转则多为先进行一次方向旋转，使其呈链状后，再进行一次反方向旋转.

如下图，为需要维护的不平衡状态.
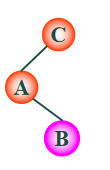
在这里插入图片描述
又如下图，为进行旋转（左旋A，B）使三点共链的状态.
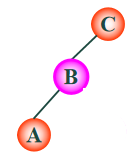
在这里插入图片描述
再如下图，为进行反方向旋转（右旋C，B）使其平衡的状态.
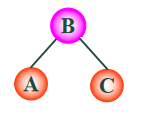
在这里插入图片描述
最后保持平衡.

因为其不同方向两次旋转的特性，所以双旋转分为左右旋（zagzig）和右左旋（zigzag）.

代码实现平衡维护 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].hi=max(tr[ls(r)].hi,tr[rs(r)].hi)+1;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+1;
}

void mountain(ll &r) // 注意引用&
{
    ll lf=ls(r),rg=rs(r); // ls(r)为表示r的左儿子的函数，rs(r)反之
    if(tr[lf].hi==tr[rg].hi+2)
    {
        if(tr[ls(lf)].hi==tr[rg].hi+1)
            rote(r,1); // 单旋转，1表示zig，0反之
        else if(tr[rs(lf)].hi==tr[rg].hi+1)
            rote2(r,0); // 双旋转，0表示zagzig，1反之
    }
    else if(tr[rg].hi==tr[lf].hi+2)
    {
        if(tr[rs(rg)].hi==tr[lf].hi+1)
            rote(r,0);
        else if(tr[ls(rg)].hi==tr[lf].hi+1)
            rote2(r,1);
    }
    pushup(r);
}

代码实现旋转操作 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].hi=max(tr[ls(r)].hi,tr[rs(r)].hi)+1;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+1;
}

void rote(ll &r,ll op)
{
    ll t=tr[r].ch[!op];
    tr[r].ch[!op]=tr[t].ch[op];
    tr[t].ch[op]=r;
    pushup(r),pushup(t);
    r=t;
}

void rote2(ll &r,ll op)
{
    rote(tr[r].ch[op],op);
    rote(r,!op);
}

小飞版来咯~

【模板】普通平衡树

Code 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define ls(r) tr[r].ch[0]
#define rs(r) tr[r].ch[1]

const ll MAXN=5e5+5,INF=0x3f3f3f3f;

struct AVL
{
    ll ch[2],sz,val,hi,cnt;
}tr[MAXN];
ll rt,pcnt;

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].hi=max(tr[ls(r)].hi,tr[rs(r)].hi)+1;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+1;
}

void rote(ll &r,ll op)
{
    ll t=tr[r].ch[!op];
    tr[r].ch[!op]=tr[t].ch[op];
    tr[t].ch[op]=r;
    pushup(r),pushup(t);
    r=t;
}

void rote2(ll &r,ll op)
{
    rote(tr[r].ch[op],op);
    rote(r,!op);
}

void mountain(ll &r)
{
    ll lf=ls(r),rg=rs(r);
    if(tr[lf].hi==tr[rg].hi+2)
    {
        if(tr[ls(lf)].hi==tr[rg].hi+1)
            rote(r,1);
        else if(tr[rs(lf)].hi==tr[rg].hi+1)
            rote2(r,0);
    }
    else if(tr[rg].hi==tr[lf].hi+2)
    {
        if(tr[rs(rg)].hi==tr[lf].hi+1)
            rote(r,0);
        else if(tr[ls(rg)].hi==tr[lf].hi+1)
            rote2(r,1);
    }
    pushup(r);
}

void ins(ll &r,ll x)
{
    if(!r)
    {
        tr[++pcnt].val=x,r=pcnt;
        pushup(r);
        return;
    }

    if(x<tr[r].val)
        ins(ls(r),x);
    else
        ins(rs(r),x);
    mountain(r);
}

ll del(ll &r,ll x)
{
    ll tmp;
    if(tr[r].val==x||x<tr[r].val&&!ls(r)||x>tr[r].val&&!rs(r))
    {
        tmp=tr[r].val;
        if(!ls(r)||!rs(r))
        {
            r=ls(r)+rs(r);
            return tmp;
        }
        tr[r].val=del(ls(r),x);
    }
    else
    {
        if(x<tr[r].val)
            tmp=del(ls(r),x);
        else
            tmp=del(rs(r),x);
    }
    mountain(r);
    return tmp;
}

ll grank(ll r,ll x)
{
    if(!r)
        return 1;
    if(x<=tr[r].val)
        return grank(ls(r),x);
    return tr[ls(r)].sz+1+grank(rs(r),x);
}

ll xth(ll r,ll x)
{
    if(tr[ls(r)].sz>=x)
        return xth(ls(r),x);
    if(tr[ls(r)].sz+1>=x)
        return tr[r].val;
    return xth(rs(r),x-tr[ls(r)].sz-1);
}

ll pre(ll r,ll x)
{
    if(!r)
        return -INF;
    if(tr[r].val>=x)
        return pre(ls(r),x);
    return max(tr[r].val,pre(rs(r),x));
}

ll nxt(ll r,ll x)
{
    if(!r)
        return INF;
    if(tr[r].val<=x)
        return nxt(rs(r),x);
    return min(tr[r].val,nxt(ls(r),x));
}

int main()
{
    ll n;
    scanf("%lld",&n);
    while(n--)
    {
        ll op,x;
        scanf("%lld%lld",&op,&x);
        if(op==1)
            ins(rt,x);
        if(op==2)
            del(rt,x);
        if(op==3)
            printf("%lld\n",grank(rt,x));
        if(op==4)
            printf("%lld\n",xth(rt,x));
        if(op==5)
            printf("%lld\n",pre(rt,x));
        if(op==6)
            printf("%lld\n",nxt(rt,x));
    }
}

Treap

介绍

虽然 AVL 敲可爱哒~
但是在考场上真的来得及打吗？

其实只要你练得够多，最快可在10min内打完，一般人也可以练进12min.

明显地，维护平衡操作太长了，可不可以省去？

或许我们用一些随机值赋值给不同节点，使其成为节点的优先级，在构造二叉查找树时使其满足点权有序性与优先级（随机值）有序性.

如果这样，随机生成的数字一般可以使二叉查找树接近平衡.可理解为相对平衡但不是绝对平衡.

当然，除非你考前被奆佬%而rp–， 一般随机值不会刚好使其变成一条链.
在大数据下更具有代表性，即维护平衡树平衡的成功概率与数据大小成正比.

所以，就有了时间复杂度不如 AVL 优秀，但是足够的—— Treap ！！

$Treap$=$Tree+Heap$.
从名字上可见它满足点权有序性（二叉查找 tree ），和优先级（随机值）有序性（大根或小根 heap ）.

平衡维护

其实 Treap 的维护与 AVL 很像，这里就不放图了.

它们之间的区别或许只是维护时的条件不同.

  • AVL 是当左右子树高度相差超过1时进行维护
  • Treap 是当左右子树优先级小于（或大于，这里不作定性要求，但是同一代码中必须都是小于或大于）根节点优先级时进行维护

还有一点，因为 Treap 讲究好写，所以只需要在插入数据的时候维护一下就可以了，删除后不用再次维护.

代码实现插入数据与维护 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

void pushup(ll r) {
    if (!r)
        return;
    tr[r].sz = tr[ls(r)].sz + tr[rs(r)].sz + 1;
}

void ins(ll &r, ll x) {
    if (!r) {
        tr[++pcnt].val = x;
        tr[pcnt].pri = rand();
        r = pcnt;
        pushup(r);
        return;
    }
    if (x < tr[r].val) {
        ins(ls(r), x);
        if (tr[ls(r)].pri > tr[r].pri)
            rote(r, 1); // 旋转操作见AVL
    } else {
        ins(rs(r), x);
        if (tr[rs(r)].pri > tr[r].pri)
            rote(r, 0);
    }
    pushup(r);
}

小飞版来咯~

【模板】普通平衡树

Code 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define ls(r) tr[r].ch[0]
#define rs(r) tr[r].ch[1]

const ll MAXN = 5e5 + 5, INF = 0x3f3f3f3f;

struct Treap {
    ll ch[2], sz, val, pri;
} tr[MAXN];
ll rt, pcnt;
ll fa[MAXN];

void pushup(ll r) {
    if (!r)
        return;
    tr[r].sz = tr[ls(r)].sz + tr[rs(r)].sz + 1;
}

void rote(ll &r, ll op) {
    ll t = tr[r].ch[!op];
    tr[r].ch[!op] = tr[t].ch[op];
    tr[t].ch[op] = r;
    pushup(r), pushup(t);
    r = t;
}

void ins(ll &r, ll x) {
    if (!r) {
        tr[++pcnt].val = x;
        tr[pcnt].pri = rand();
        r = pcnt;
        pushup(r);
        return;
    }
    if (x < tr[r].val) {
        ins(ls(r), x);
        if (tr[ls(r)].pri > tr[r].pri)
            rote(r, 1);
    } else {
        ins(rs(r), x);
        if (tr[rs(r)].pri > tr[r].pri)
            rote(r, 0);
    }
    pushup(r);
}

ll del(ll &r, ll x) {
    ll tmp;
    // 解释一下，因为平衡树是一种二叉查找树，
    // 所以可以把叶子结点与“要删除节点”换一下位置，
    // 这样的话二叉查找树的性质不会被改变，
    // 也成功地删除了节点（其他版本的平衡树删除维护同理）
    if (x == tr[r].val || x < tr[r].val && !ls(r) || x > tr[r].val && !rs(r)) {
        tmp = tr[r].val;
        if (!ls(r) || !rs(r)) {
            r = ls(r) + rs(r);
            return tmp;
        }
        tr[r].val = del(ls(r), x);
    } else {
        if (x < tr[r].val)
            tmp = del(ls(r), x);
        else
            tmp = del(rs(r), x);
    }
    pushup(r);
    return tmp;
}

ll grank(ll r, ll x) {
    if (!r)
        return 1;
    if (x <= tr[r].val)
        return grank(ls(r), x);
    return tr[ls(r)].sz + 1 + grank(rs(r), x);
}

ll xth(ll r, ll x) {
    if (tr[ls(r)].sz >= x)
        return xth(ls(r), x);
    if (tr[ls(r)].sz + 1 >= x)
        return tr[r].val;
    return xth(rs(r), x - 1 - tr[ls(r)].sz);
}

ll pre(ll r, ll x) {
    if (!r)
        return -INF;
    if (tr[r].val >= x)
        return pre(ls(r), x);
    return max(tr[r].val, pre(rs(r), x));
}

ll nxt(ll r, ll x) {
    if (!r)
        return INF;
    if (tr[r].val <= x)
        return nxt(rs(r), x);
    return min(tr[r].val, nxt(ls(r), x));
}

int main() {
    srand(time(0));
    ll n;
    scanf("%lld", &n);
    while (n--) {
        ll op, x;
        scanf("%lld%lld", &op, &x);
        if (op == 1)
            ins(rt, x);
        if (op == 2)
            del(rt, x);
        if (op == 3)
            printf("%lld\n", grank(rt, x));
        if (op == 4)
            printf("%lld\n", xth(rt, x));
        if (op == 5)
            printf("%lld\n", pre(rt, x));
        if (op == 6)
            printf("%lld\n", nxt(rt, x));
    }

    return 0;
}

FHQ Treap

介绍

可以说，旋转操作是占主流算法的大多数.

但是一旦牵扯到可连续性等方面乃至理解方面，旋转操作是不太可取的.

于是范浩强奆佬就发明了不用旋转的 Treap 算法—— FHQ Treap ！！
也称作无旋 Treap.

不旋转，怎么维护平衡？

分裂！！

合并！！

分裂操作与合并操作

分裂split

分裂操作split是最难理解的也是最关键的一步.

我们在插入数据和删除数据需要找到一个合适的点.
而找这个点的路径，可以把树分裂成两部分，把小于等于插入值的分裂到左树，大于的就分裂到右树.

就这样，我们可以得到两棵树（也有可能是空树）.

合并merge

合并操作的对象是两棵树，这两棵树一定满足，左边的树权最大值小于右边的树的权值最小值.

我们根据其优先级来合并.
为了描述方面，我们设左边的树为 $L$，右边的树为 $R$.
首先比较两棵树的树根，谁优先级小，谁就作为新的树根.
假设 $L$ 的优先级较小，那么 $L$ 的根做新的树根，则问题转换为 $L$ 的右子树与 $R$ 的合并问题了；否则就是 $R$ 的根作为新树的根，问题转换为 $L$ 和 $R$ 的左子树的合并问题了.

明显地，可以写成递归.
这样递归下去，直到某棵树为空，则递归结束。

代码实现split与merge 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+1;
}

void split(ll r,ll &xrt,ll &yrt,ll v)
{
    // r为需要分裂的树的根
    // xrt为分裂后将得到左树的树根
    // yrt反之
    if(!r)
        xrt=yrt=0;
    else if(v<tr[r].val)
    {
        yrt=r;
        split(ls(r),xrt,ls(r),v);
    }
    else
    {
        xrt=r;
        split(rs(r),rs(r),yrt,v); // 等于v的节点分到左树里
    }
    pushup(r);
}

void merge(ll &r,ll xrt,ll yrt)
{
    // r为合并后的新根
    // xrt为参与合并的左子树的根
    // yrt反之
    if(!xrt||!yrt)
        r=xrt+yrt;
    else if(tr[xrt].pri<tr[yrt].pri)
    {
        r=xrt;
        merge(rs(r),rs(r),yrt);
    }
    else
    {
        r=yrt;
        merge(ls(r),xrt,ls(r));
    }
    pushup(r);
}

小飞版来咯~

【模板】普通平衡树

Code 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define rep(c,i,a,b) for(c i=a;i<=b;++i)
#define per(c,i,a,b) for(c i=a;i>=b;--i)
#define ls(r) tr[r].ch[0]
#define rs(r) tr[r].ch[1]

const ll MAXN=5e5+3,INF=0x3f3f3f3f;

struct FHQ_Treap
{
    ll ch[2];
    ll sz;
    ll val;
    ll pri;
}tr[MAXN];
ll pcnt,rt,rt1,rt2;

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+1;
}

void split(ll r,ll &xrt,ll &yrt,ll v)
{
    if(!r)
        xrt=yrt=0;
    else if(v<tr[r].val)
    {
        yrt=r;
        split(ls(r),xrt,ls(r),v);
    }
    else
    {
        xrt=r;
        split(rs(r),rs(r),yrt,v);
    }
    pushup(r);
}

void merge(ll &r,ll xrt,ll yrt)
{
    if(!xrt||!yrt)
        r=xrt+yrt;
    else if(tr[xrt].pri<tr[yrt].pri)
    {
        r=xrt;
        merge(rs(r),rs(r),yrt);
    }
    else
    {
        r=yrt;
        merge(ls(r),xrt,ls(r));
    }
    pushup(r);
}

void ins(ll &r,ll x)
{
    split(r,rt1,rt2,x);
    tr[++pcnt].val=x,tr[pcnt].pri=rand(),tr[pcnt].sz=1,r=pcnt;
    merge(rt1,rt1,pcnt);
    merge(r,rt1,rt2);
}

void del(ll &r,ll x)
{
    ll rt3;
    split(r,rt1,rt2,x);
    split(rt1,rt1,rt3,x-1);
    merge(rt1,rt1,rt3);
    merge(r,rt1,rt2);
}

ll getrank(ll r,ll x) // 数x的排名
{
    if(r==0)
        return 1;
    if(tr[r].val<x)
        return tr[ls(r)].sz+1+getrank(rs(r),x);
    return getrank(ls(r),x);
}

ll xth(ll r,ll x) // 第x个数
{
    if(tr[ls(r)].sz>=x)
        return xth(ls(r),x);
    if(tr[ls(r)].sz+1>=x)
        return tr[r].val;
    return xth(rs(r),x-tr[ls(r)].sz-1);
}

ll getpre(ll r,ll x) // x的前驱
{
    if(r==0)
        return -INF;
    if(x<=tr[r].val)
        return getpre(ls(r),x);
    return max(tr[r].val,getpre(rs(r),x));
}

ll getnxt(ll r,ll x) // x的后继
{
    if(r==0)
        return INF;
    if(x>=tr[r].val)
        return getnxt(rs(r),x);
    return min(tr[r].val,getnxt(ls(r),x));
}

int main()
{
    srand(time(0));
    ll n;
    scanf("%lld",&n);
    while(n--)
    {
        ll op,x;
        scanf("%lld%lld",&op,&x);
        if(op==1)
            ins(rt,x);
        if(op==2)
            del(rt,x);
        if(op==3)
            printf("%lld\n",grank(rt,x));
        if(op==4)
            printf("%lld\n",xth(rt,x));
        if(op==5)
            printf("%lld\n",pre(rt,x));
        if(op==6)
            printf("%lld\n",nxt(rt,x));
    }
    return 0;
}

Splay

介绍

Splay 也称为伸展树，它也满足二叉查找树的性质.
即一个节点的左子树的所有点权都会小于当前节点，右子树反之.

它和其他平衡树算法最大不同的是，它不需要主动维护平衡，我们只需要在每个操作结束后进行一次splay(x,goal)的操作，它就可以自己维护了.

当然splay(x,goal)里面还是有旋转操作的.

splay(x,goal)伸展操作

splay(x,goal)操作也就是伸展操作.

通过一系列旋转使得 x 转到 goal 节点，旋转也需要分情况而论.
以下 goal 节点为 root 根节点举例.

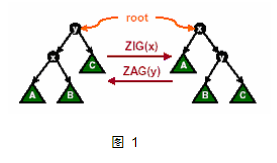
情况一：节点 x 的父节点 y 是根节点. 这时如果 x 是 y 的左儿子，则进行一次 zig 操作；反之同理. 如图 1 所示.

在这里插入图片描述

情况二：节点x的父节点y还有一个父节点z. 且此时三点成链，则进行一次zigzig操作或zagzag操作（是的，此处旋转不需要维护平衡，只是为了将x旋转到目标节点），如图2所示.

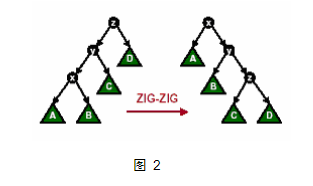
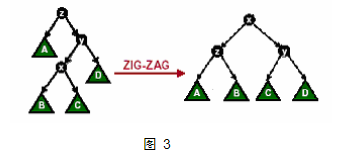
在这里插入图片描述

情况三：节点x的父节点y还有父节点z. 且此时三点呈“之”字形，则进行一次zagzig操作或zigzag操作，如图3所示.

在这里插入图片描述

如图5，是一次splay(2,rt)的操作.

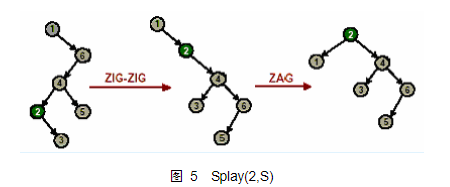
在这里插入图片描述

明显地，经过 splay() 操作后，平衡树明显“平衡”了许多.
所以我们在一些插入、查询等操作后就做一遍 splay().

这样做的话，时间复杂度可以下降. 但是同样地，常数也就增加了. 所以 Splay 算法是本文 4 个算法中最慢的.

代码实现 splay(x,goal) 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+tr[r].cnt;
}

void rote(ll x)
{
    ll y=fa[x],z=fa[y],flg=(x==rs(fa[x]));
    tr[y].ch[flg]=tr[x].ch[!flg];
    if(tr[x].ch[!flg]) fa[tr[x].ch[!flg]]=y;
    tr[x].ch[!flg]=y;
    fa[y]=x;
    fa[x]=z;
    if(z) tr[z].ch[y==rs(z)]=x;
    pushup(y),pushup(x);
}

void splay(ll x,ll goal) // 这里goal==0时，表示将x转到根节点
{
    // 这里3行包含了旋转的3种情况，请自行理解，这里不作过多解释
    for(ll y;(y=fa[x])!=goal;rote(x)) 
        if(fa[y]!=goal)
            rote( ( ( rs(fa[y])==y) == (rs(y)==x) ) ? y : x);
    if(goal==0) // 如果目标是根节点，那根节点需要更新为x
        rt=x;
}

小飞版来咯~

【模板】普通平衡树

Code 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define ls(r) tr[r].ch[0]
#define rs(r) tr[r].ch[1]

const ll MAXN=5e5+5,INF=0x3f3f3f3f;

struct Splay
{
    ll ch[2],sz,val,cnt;
}tr[MAXN];
ll rt,pcnt;
ll fa[MAXN];

void pushup(ll r)
{
    if(!r)
        return;
    tr[r].sz=tr[ls(r)].sz+tr[rs(r)].sz+tr[r].cnt;
}

void rote(ll x)
{
    ll y=fa[x],z=fa[y],flg=(x==rs(fa[x]));
    tr[y].ch[flg]=tr[x].ch[!flg];
    if(tr[x].ch[!flg]) fa[tr[x].ch[!flg]]=y;
    tr[x].ch[!flg]=y;
    fa[y]=x;
    fa[x]=z;
    if(z) tr[z].ch[y==rs(z)]=x;
    pushup(y),pushup(x);
}

void splay(ll x)
{
    for(ll y;(y=fa[x]);rote(x))
    if(fa[y]) rote(((rs(fa[y])==y)==(rs(y)==x))?y:x);
    rt=x;
}

void ins(ll x)
{
    if(!rt)
    {
        tr[++pcnt].val=x;
        tr[pcnt].cnt++;
        rt=pcnt;
        pushup(rt);
        return;
    }
    ll cur=rt,f=0;
    while(1)
    {
        if(tr[cur].val==x)
        {
            tr[cur].cnt++;
            pushup(cur);
            pushup(f);
            splay(cur);
            return;
        }
        f=cur;
        cur=tr[cur].ch[tr[cur].val<x];
        if(!cur)
        {
            tr[++pcnt].val=x;
            tr[pcnt].cnt++;
            fa[pcnt]=f;
            tr[f].ch[tr[f].val<x]=pcnt;
            pushup(pcnt);
            pushup(f);
            splay(pcnt);
            return;
        }
    }
}

ll grank(ll x)
{
    ll res=0,cur=rt;
    while(1)
    {
        if(tr[cur].val>x)
            cur=ls(cur);
        else
        {
            res+=tr[ls(cur)].sz;
            if(tr[cur].val==x)
            {
                splay(cur);
                return res+1;
            }
            res+=tr[cur].cnt;
            cur=rs(cur);
        }
    }
}

ll xth(ll x)
{
    ll cur=rt;
    while(1)
    {
        if(ls(cur)&&tr[ls(cur)].sz>=x)
            cur=ls(cur);
        else
        {
            x-=tr[ls(cur)].sz+tr[cur].cnt;
            if(x<=0)
            {
                splay(cur);
                return tr[cur].val;
            }
            cur=rs(cur);
        }
    }
}

ll pre()
{
    ll cur=ls(rt);
    if(!cur)
        return 0;
    while(rs(cur)) cur=rs(cur);
    splay(cur);
    return cur;
}

ll nxt()
{
    ll cur=rs(rt);
    if(!cur)
        return 0;
    while(ls(cur)) cur=ls(cur);
    splay(cur);
    return cur;
}

void del(ll x)
{
    grank(x);
    if(tr[rt].cnt>1)
    {
        tr[rt].cnt--;
        splay(rt);
        return;
    }
    if(!rs(rt)&&!ls(rt))
    {
        rt=0;
        return;
    }
    if(!ls(rt)||!rs(rt))
    {
        rt=ls(rt)+rs(rt);
        fa[rt]=0;
        return;
    }
    ll cur=rt;
    ll y=pre();
    fa[rs(cur)]=y;
    rs(y)=rs(cur);
    pushup(rt);
}

int main()
{
    ll n;
    scanf("%lld",&n);
    while(n--)
    {
        ll op,x;
        scanf("%lld%lld",&op,&x);
        if(op==1)
            ins(x);
        if(op==2)
            del(x);
        if(op==3)
            printf("%lld\n",grank(x));
        if(op==4)
            printf("%lld\n",xth(x));
        if(op==5)
            ins(x),printf("%lld\n",tr[pre()].val),del(x);
        if(op==6)
            ins(x),printf("%lld\n",tr[nxt()].val),del(x);
    }

    return 0;
}

最后

本文写得还是很仓促的，有些漏洞大家原谅一下.(^^)

本文还有很多不完善的地方，例如 AVL 代码没有指针版、图片模糊等.
欢迎大家在评论区留下建议或疑问、收藏、转发学习.

转载请注明出处.
仅供参考、学习用，不商用.

The End