浅谈基数排序
前言
注意,本贴的算法是基数排序而不是计数排序。这两者差别不大,但是存在着一定差异。
一句话做法
从低位到高位,每次都把所有要排序的数(含前导 $0$)丢入相应的桶($0$~$9$),再从小到大(对于桶的编号而言从小到大)取出来,一定次数后,原数组有序。
数据模拟
假如要对以下几个数排序。
|
|
第一轮,看个位
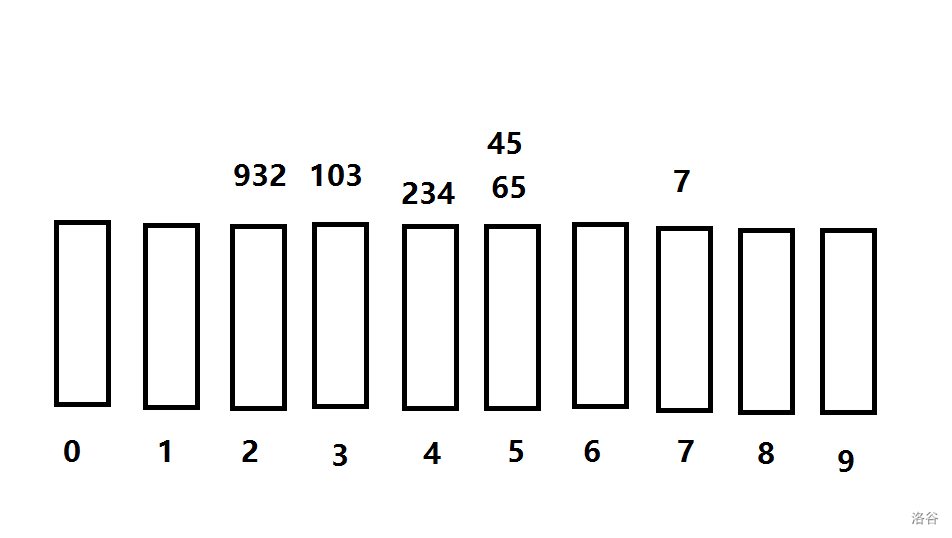
此刻数组为:
|
|
第二轮,看十位
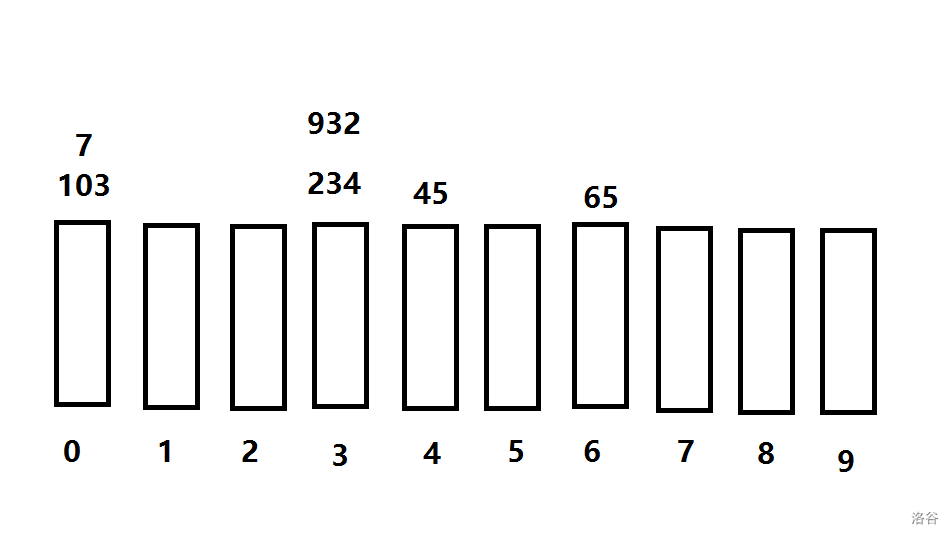
此刻数组为:
|
|
第三轮,看百位
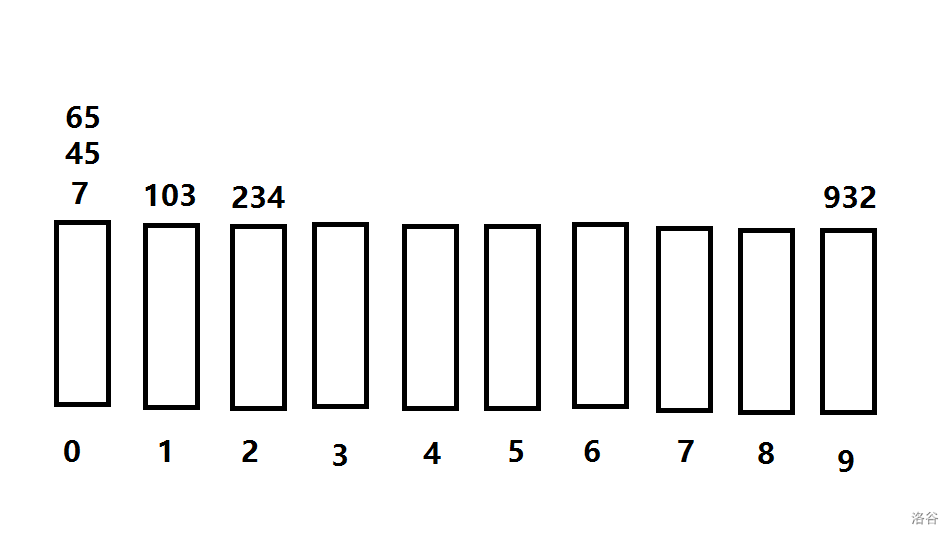
此刻数组为:
|
|
此时尽管数组已经有序,但过程并未完整。因为对于一些数据是不一定如此凑巧提前就能排好序的。
第四轮,看千位
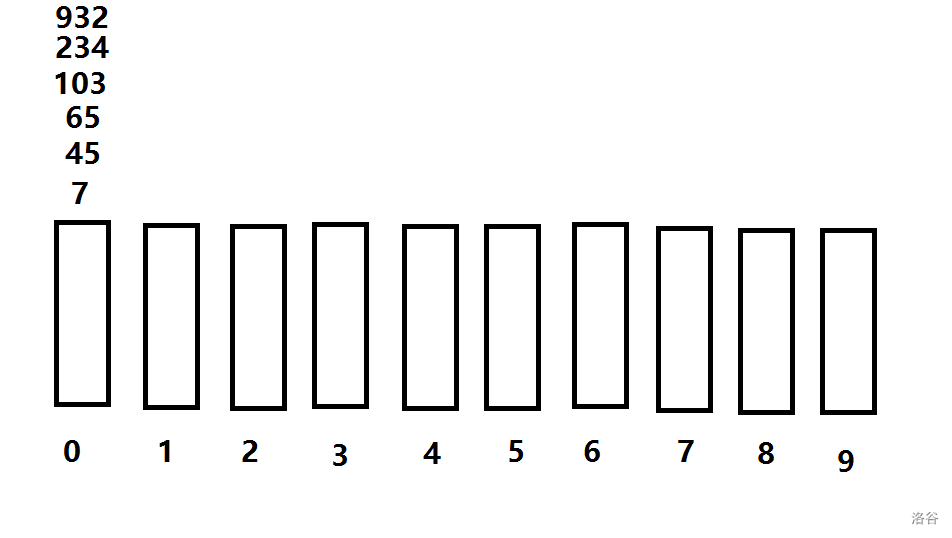
此刻数组为:
|
|
数组已经有序。
证明
注:以下考虑正整数。“数字”是 $[0,9]$ 之间的,“数”是 $[0,+\infty)$。
在小学一年级的时候,我们就已学过如何比较数之间的大小。
首先看数的位数,位数大的,肯定较大。
其次从高到低比较每位上的数字大小,一直到不等的时候,哪个数字大,那个数就大。
因此,基数排序的原理也是一样的。
首先从最低位开始放,就可以确定当前位的数字的相对大小关系。
然后考虑再高一位的时候(不妨称为“升位”),那些位数不够的数就会全部放入 $0$ 的桶里。
由于我们是按从小到大的顺序将不同的桶的元素放入 $0$ 号桶,所以保证了“桶底”的一定是最小的。