浅谈 ST 表

这种东西还是很简单的，但是涉及左移右移，模板容易打挂，写篇笔记。

ST 表是什么

虽然这个是通过二维数组来实现的，但是我不是很喜欢称之为“表”。我觉得完全可以看作是在一维序列上的区间，看作“表”的话关联性就会很鬼畜。

其主要思想是：$f[i][j]$ 表示区间左端点为 $i$，区间长度为 $2^j$ 的区间信息（可以是最大值、区间和、区间 $\gcd$ 等）。

有人说了，那为什么不用线段树？

我一开始也是这么想的，所以我一开始有段时间只会线段树，不会 ST 表。

ST 表的好处在于，他可以 $O(1)$ 查询区间信息。至于预处理，就是 $O(n\log n)$ 的。

而线段树，基本任何操作都是 $O(\log n)$ 的。

所以如果你想 $O(1)$ 查询，那就要学 ST 表。

注意！ ST 表并不支持带修改。也就是说，对于不会修改的题目，并且需要查询时间优秀的题目，ST 表才有比线段树明显的优势。

如何实现 ST 表

预处理

众所周知，如果一个区间的长度是 $1$，那么这个“区间”就是 $1$ 个元素。所以可以直接：

code

1

for(int i=1;i<=n;i++) f[i][0]=a[i];

接下来考虑区间长度为 $2^j$ 的区间。

为什么我们要令长度是 $2^j$ 而不是 $j$ 呢？——这正是这个算法的精髓所在。

因为长度为 $2^j$ 的区间可以看做由两个长度为 $2^{j-1}$ 组成，而当我们正要处理出 $f[i][j]$ 的时候，肯定已知 $f[i][j-1]$ （因为我们通过递推得出 $f$），所以可以直接转换。

此处实现代码以维护区间和为例。

code

1
2
3
4
5
6
7


for(int j=1;(1<<j)<=n;j++)
{
    for(int i=1;i+(1<<j)-1<=n;i++)
    {
        f[i][j]=f[i][j-1]+f[i+(1<<(j-1))][j-1];
    }
}

转换没看懂？

看个图吧

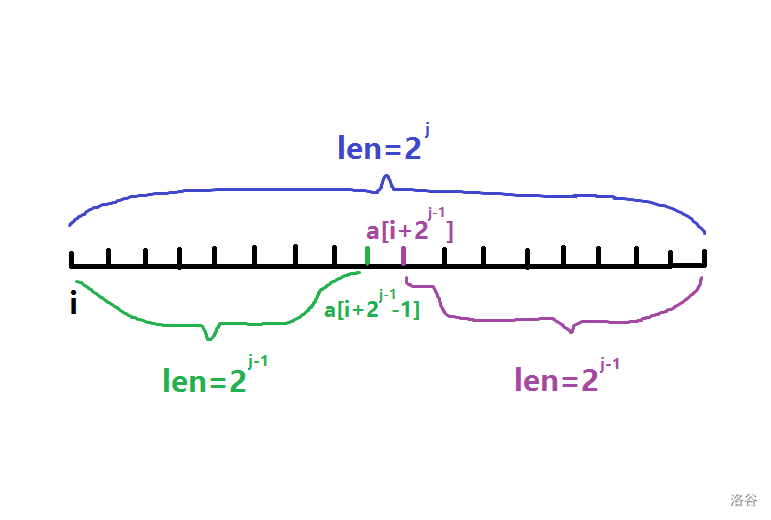
（图中一个“棍棍”就是一个元素）

查询

查询亦是同理，只不过我们 $f[i][j]$ 中的 $i$ 是开头，$l$ 就直接放进去，$r$ 就要减去区间长度再 $+1$ 来得到开头。

这里依然是以区间和为例。

code

1
2
3
4
5


int query(int l,int r)
{
    int k=log2(r-l+1);
    return f[l][k]+f[r-(1<<k)+1][k];
}

P3865 【模板】ST 表

code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#include<bits/stdc++.h>
using namespace std;

#define int long long

const int MAXN=1e5+5;

int n,m;
int a[MAXN];
int lg[MAXN];
int f[MAXN][30];

inline int rd()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
        x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return x*f;
} 

int query(int l,int r)
{
    int k=lg[r-l+1];
    int d=r-(1<<k)+1;
    return max(f[l][k],f[d][k]);
}

signed main()
{
    n=rd(),m=rd();
    for(int i=1;i<=n;i++)
        a[i]=rd();
    for(int i=1;i<=n;i++)
        f[i][0]=a[i];
    for(int i=2;i<=n;i++)
        lg[i]=lg[i>>1]+1;
    for(int j=1;j<=lg[n];j++)
    {
        for(int i=1;i<=n-(1<<j)+1;i++)
        {
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
        }
    }
    while(m--)
    {
        int l=rd(),r=rd();
        printf("%lld\n",query(l,r));
    }
    return 0;
}