超级简单的后缀数组（SA）！！

前言

这里选择当一手标题党。

由于刚学完这个字符串算法，本人字符串算法又比较薄弱，好不容易这一次在晚修看各种资料看得七七八八，决定趁脑子清醒的时候记录下来。

免得自己不久后忘了后又要痛苦地再看各种资料。希望这篇博客能帮到你。

前置知识：RMQ 问题、基数排序、lcp 问题

使用指南：在抽象的时候，可以选择先不看证明；先记住结论，顺一遍后再返回来补证明也是可以的。如果有草稿本和笔，是最佳的选择。

到底什么是“后缀数组”？

后缀，顾名思义，即为 $[i,..,n]$ 的区间。以 $S$ 的第 $i$ 个字符开始的后缀定义为 $\text{Suffix}(i)$，下文简写为 $\text{suf}(i)$。

如果这玩意儿（后缀）碰上了字符串，那么后缀也就成了特殊的字串。

后缀数组又是什么呢？

“后缀数组——处理字符串的有力工具。”——国集选手罗穗骞

说到底，这是一个处理字符串的基础算法。

学会 后缀自动机（SAM） 之后是不是就可以不学 后缀数组（SA） 了？不！虽然 SAM 更为强大和全面，但是有些问题 SA 将体现出优势，只单方面地掌握 SAM 是远远不够的。

例子：求一个串后缀的 lcp 方面的应用，SA 可以直接用 RMQ，但是 SAM 还要求出 LCA。等等。

那现在让我们开始吧。

后缀数组与名次数组

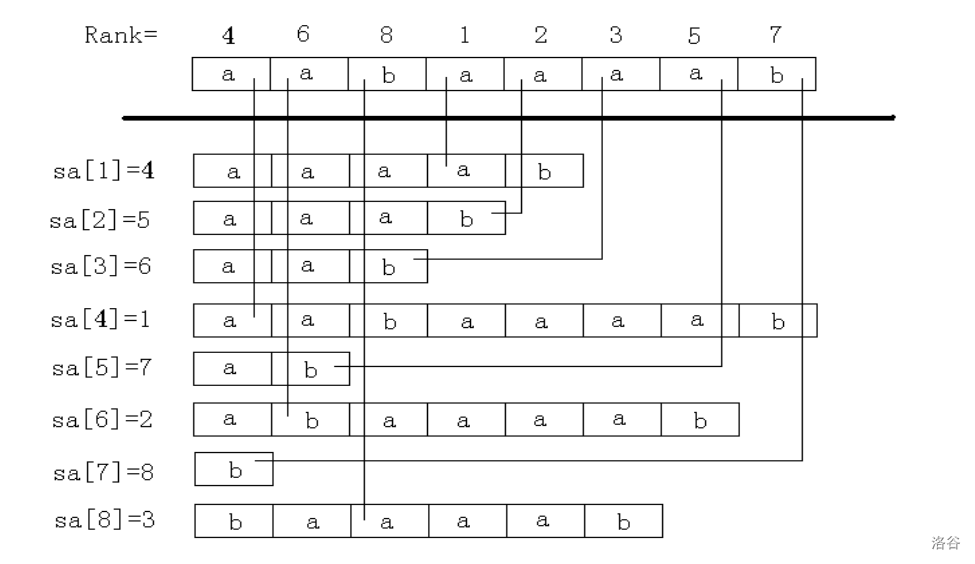
此“后缀数组”非彼“后缀数组”，此二级标题中的“后缀数组”是一个实打实的数组。定义为：$\text{SA}[i]$，存储的是 $1,…,n$ 的一个排列。

他保证 $\text{suf}(\text{SA}[i])<\text{suf}(\text{SA}[i+1])$，就是将 $S$ 的后缀从小到大排序后把后缀的开头按序放入 $\text{SA}$ 中。

名次数组 $\text{Rank[i]}$ 存储的是 $\text{suf}(i)$ 在所有后缀中排序后的名次。

一言了之，$\text{SA}[i]$ 表示原串中从小到大排名为 $i$ 的是哪个后缀；$\text{Rank}[i]$ 表示原串中后缀 $i$ 从小到大排名后的名次。

“简单的说，后缀数组是‘排第几的是谁？’，名次数组是‘你排第几？’。”——罗穗骞

显然，这俩玩意儿就是双映射关系，说白了就是运算互逆。

怎么求出这两个数组？——倍增算法

大家都可以想到的朴素算法或时间复杂度不优秀的算法这里就不再提及了。

由于过于复杂的 $\text{DC3}$算法本人又不会，所以这里只提及 $\text{O}(n \log n)$ 的倍增算法。

主要思路：对每个字符开始长度为 $2^k$ 的子串进行排序，求出 $\text{Rank}$ 值。

$k$ 从 $0$ 开始，每次不断 $+1$ 直到长度超过了原串的长度（$2^k>n$）。当达到限制后，每个字符开始的长度为 $2^k$ 的子串便相当于所有的后缀。并且此时肯定已经得到了互不相等的 $\text{Rank}$ 值。

此刻要解决的是如何排序。

如果采用 sort 快排，时间复杂度并没有利用字符串后缀的性质。

我们在处理长为 $2^k$ 的问题时，肯定是已经知道 $2^{k-1}$ 的 $\text{Rank}$ 值。那我们就可以利用这些值，把一个子串 $\text{Sub}(i,2^k)$ （从 $i$ 开始长度为 $2^k$ 的串），看作由两个关键字组成：$\text{Sub}(i,2^{k-1})+\text{Sub}(i+2^{k-1},2^{k-1})$。由此，可用基数排序。

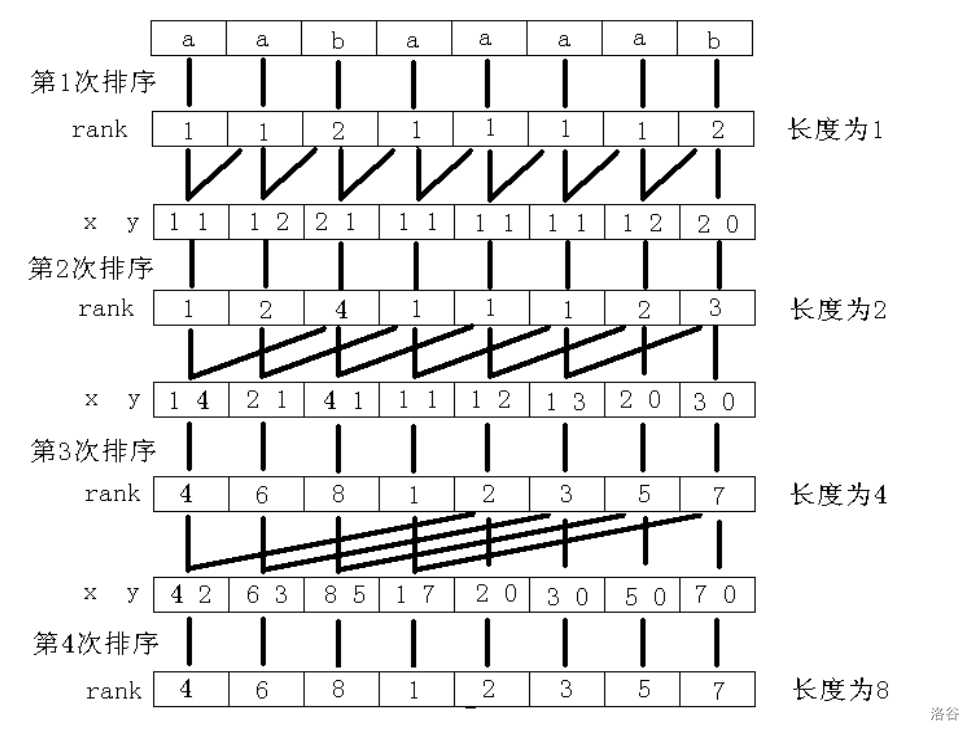
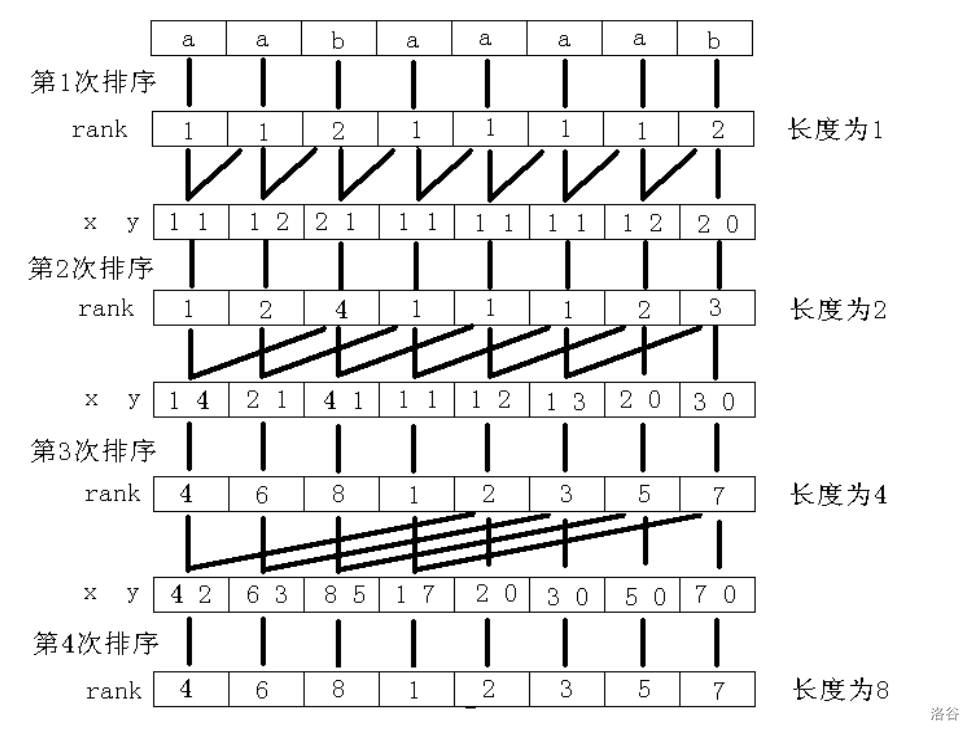
举个例子：

以字符串“aabaaaab”为例，整个过程如图所示。其中 $x,y$ 是表示长度为 $2^k$ 的字符串的两个关键字。

怎么样？这个图看不懂？静下心来，细细揣摩。这里要嚼透了（尤其是 $\text{SA},\text{Rank}$ 数组的差别），才能理解后面更为抽象的代码实现。

求 SA 代码具体实现

以往很多算法都是贴个模板 code 就走人了，但今天不行。

放一下板子，你们就明白（为什么不行）了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


int sa[MAXN],rk[MAXN],oldrk[MAXN<<1],id[MAXN],key1[MAXN],cnt[MAXN];
bool cmp(int x,int y,int w)
{return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w];}
void SA()
{
    for(int i=1;i<=n;i++) ++cnt[rk[i]=s[i]];
    for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--) sa[cnt[rk[i]]--]=i;
    int p;
    for(int w=1;;w<<=1,m=p)
    {
        p=0;
        for(int i=n;i>=n-w+1;i--) id[++p]=i;
        for(int i=1;i<=n;i++)
            if(sa[i]>w)
                id[++p]=sa[i]-w;
        for(int i=1;i<=m;i++) cnt[i]=0;
        for(int i=1;i<=n;i++)
            ++cnt[key1[i]=rk[id[i]]];
        for(int i=1;i<=m;i++)
            cnt[i]+=cnt[i-1];
        for(int i=n;i>=1;i--)
            sa[cnt[key1[i]]--]=id[i];
        for(int i=1;i<=n;i++) oldrk[i]=rk[i];
        p=0;
        for(int i=1;i<=n;i++)
            rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
        if(p==n) break;
    }
}

如果你能直接看懂此代码是如何求出 $\text{SA}$ 数组——

那么您可以直接离开此寒舍了。并接受在下一膜拜~ Orz

如果你留了下来，别着急，我来分步讲解。

对长度为 $1$ 的子串排序

1
2
3


for(int i=1;i<=n;i++) ++cnt[rk[i]=s[i]];
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--) sa[cnt[rk[i]]--]=i;

第 1 行，就是把长为 $1$ 的子串（就是字符啦）全部扔进桶里。

第 2 行，把这个桶转换成前缀和，就可以知道字符 $i$ 在原串是第几个了。

第 3 行，由于桶内的元素也要分个排名，所以这里的写法选择了倒序循环、cnt--。

其实这 3 行就是在做基数排序

对长度为 $w$ 的子串排序

先搞定第二关键字的排序

1
2
3


p=0;
for(int i=n;i>=n-w+1;i--) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;

第 2 行，先把那些以自己开头，长度不足 $w$ 的 $i$ 放在排序数组 $id$ 的前端。这是因为他们根本没有第二关键字，可视为 $0$，自然是最小的。这里倒不倒序是一样的，你也可以正序写。

第 3 行，把那些有第二关键字的，记录他们第一关键字的开头，即 sa[i]-w。

分析一下，第 2 行的操作其实也是在记录第一关键字的开头。

处理出新的 SA 数组

1
2
3
4


for(int i=1;i<=m;i++) cnt[i]=0;
for(int i=1;i<=n;i++) ++cnt[key1[i]=rk[id[i]]];
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--) sa[cnt[key1[i]]--]=id[i];

第 1 行，置空 $\text{cnt}$，当然可以 memset(cnt,0,sizeof(cnt))。

第 2-3 行，性质上是等价于对单个字符处理出 $\text{SA}$ 的操作的，都是在做基数排序。这里的 key1[i]=rk[id[i]] 是一个减少访问空间来节约时间的小 Trick（因为第 4 行再次出现 key1[i]）。注意这里 $key1[i]\neq i$，这是因为此刻的 $\text{Rank}$ 并非此轮的新值，而是上一轮的旧值。

第 4 行，处理出新的 $\text{SA}$ 数组。

根据新的 SA 得出新的 Rank

1
2
3
4


for(int i=1;i<=n;i++) oldrk[i]=rk[i];
p=0;
for(int i=1;i<=n;i++) rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
if(p==n) break;

第 1 行，之所以要拷贝一份上一轮的 $\text{Rank}$，这是因为在得到新的 $\text{Rank}$ 时，需要上一轮的值。但是为了避免冲突，这里才会拷贝出一份。当然，代码你也可以写成 memcpy(oldrk+1,rk+1,n*sizeof(int))。

第 2-3 行，得出新值。注意，由于 $\text{Rank}$ 是可能有相同的，所以需要比较两个字符串是否完全相同。即 cmp(sa[i],sa[i-1],w)。

第 4 行，由于 $p$ 表示不同的字符串的个数，所以一旦 $p=n$，意味着再没有相同的字符串，再往下做排序已不会改变 $\text{Rank}$ 值。例如下图，第 4 次排序就是没有必要的。

for 循环为什么这么写？

1

for(int w=1;;w<<=1,m=p)

变量 $w$ 代表长度，这里不多说了。至于这个 m=p，首先要明确的一点是，$m$ 表示桶可装的元素最大值。而排序后，$\text{Rank}$ 数组中的最大值小于 $p$，所以可以改变最大值。也就是优化基数排序值域。

一些常数优化 Trick

第二关键字无需基数排序。正如代码中所打，按照他的实质，把无第二关键字的丢到最前面，再把剩下的依次放入。
优化基数排序的值域。代码中的 $p$ 即是 $\text{Rank}$ 的值域，可以优化值域。
利用 $\text{key1}$ 数组存储，减少不连续内存访问。这个在大数据效果明显。
利用 $\text{cmp}()$ 代替计算。原理同 3。
利用指针直接交换的性质。 在 $\text{oldrank}$ 数组拷贝时，是循环拷贝，常数较大。如果在定义时定义成指针形式，那就可以直接 t=x,x=y,y=t 进行一步交换。（但是这玩意儿很容易打错，编译器的警告也奇奇怪怪，慎用！！）

注：本贴提供的局部代码，除第 5 点外，其余 4 点均已运用。

这个后缀数组能干什么？

在上文，我们用了大量的篇幅来介绍什么是后缀数组、怎么代码实现求出后缀数组。那我们学会了后缀数组后，能用它解决什么问题呢？

现在回答这个问题还为之过早。要想理解后缀数组的应用，先来了解一下 $\text{height}$ 数组。

什么是 $\text{height}$ 数组

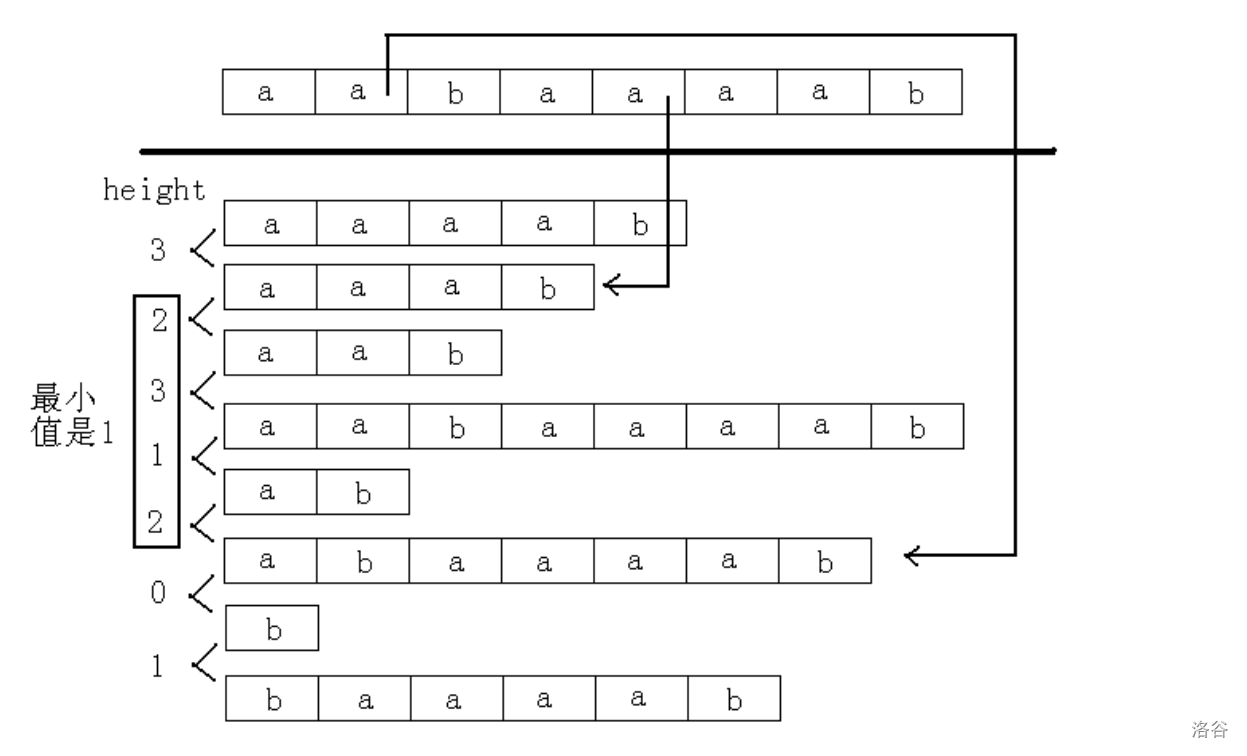
定义 $\text{height}[i]=\text{lcp}(\text{suf}(\text{SA}[i-1]),\text{suf}(\text{SA}[i]))$，$\text{lcp}(a,b)$ 即为 $a$ 和 $b$ 的最长公共前缀。

对于 $j,k(\text{Rank}[j]<\text{Rank}[k])$，有以下性质：

$$ \text{lcp}(\text{suf}(j),\text{suf}(k))=\min\{\text{height}[\text{Rank}[j]+1],...,\text{height}[\text{Rank}[k]]\} $$

以字符串 aabaaaab，求 abaaaab 和 aaab 的最长公共前缀为例：

如何高效得到 $\text{height}$ 数组？

如果直接从 $\text{height}[2]$ 计算到 $\text{height}[n]$，时间复杂度是 $\text{O}(n^2)$ 的。并没有利用上字符串的一些性质。

如果我们定义数组 $\text{h}[i]=\text{height}[\text{Rank}[i]]$，也就是 $\text{suf}(i) $ 和他前一名的后缀的最长公共前缀。将有以下性质：

$$ \text{h}[i]\geq \text{h}[i-1]-1 $$

考虑证明（这里借鉴了 oi-wiki）：

如果你不想看证明，或者看不懂，可以跳到 一个方向 部分。

当 $\text{height}[\text{Rank}[i-1]]\leq 1$ 时，不等式成立（右边 $\leq 0$）。

当 $\text{height}[\text{Rank}[i-1]] >1$ 时：

根据定义，转化为：
$$ > \text{lcp}(\text{SA}[\text{Rank}[i-1]],\text{SA}[\text{Rank}[i-1]-1]) > 1 > $$
既然 $\text{suf}(i),\text{suf}(\text{SA}[\text{Rank}[i-1]-1])$ 有长度为 $\text{height}[\text{Rank}[i-1]]$ 的最长公共前缀。

不妨设这个前缀为 $aA$，即一个字符和一个长为 $\text{height}[\text{Rank}[i-1]]-1$ 的非空字符串。

那么 $\text{suf}(i-1)=aAD$，$\text{suf}(\text{SA}[\text{Rank}[i-1]-1])=aAB$。（$B<D$，$B$ 或为空串，$D$ 非空）

因此，$\text{suf}(i)=AD$，$\text{suf}(\text{SA}[\text{Rank}[i-1]-1]+1)=AB$。

因为 $\text{suf}(\text{SA}[\text{Rank}[i]-1])$ 在大小排名上仅比 $\text{suf}(\text{SA}[\text{Rank}[i]]))$（即 $\text{suf}(i)$）少一位，而 $AB<AD$。

所以 $AB\leq \text{suf}(\text{SA}[\text{Rank}[i]-1])<AD$，显然 $\text{suf}(i)$ 与 $\text{suf}(\text{SA}[\text{Rank}[i]-1])$ 有公共前缀 $A$。

于是可得，$\text{lcp}(i,\text{SA}[\text{Rank}[i-1]])$ 至少是 $\text{height}[\text{Rank}[i-1]]-1$。

即 $\text{height}[\text{Rank}[i]]\geq \text{height}[\text{Rank}[i-1]]-1$。

令 $\text{h}[i]=\text{height}[\text{Rank}[i]]$，则
$$ \text{h}[i]\geq \text{h}[i-1]-1 > $$
证毕。

一个方向

得知此性质后，我们就有了明确的方向。按照 $\text{h}[1],…,\text{h}[n]$ 的顺序计算，并利用 $\text{h}$ 数组的性质。时间复杂度为 $\text{O}(n)$。

代码实现获得 $\text{height}$ 数组

1
2
3
4
5
6


for (i = 1, k = 0; i <= n; ++i) {
  if (rk[i] == 0) continue;
  if (k) --k;
  while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
  height[rk[i]] = k;
}

这里 $k$ 不会超过 $n$，最多减 $n$ 次，所以最多加 $2n$ 次，复杂度 $\text{O}(n)$。

$\text{height}$ 数组能干些什么——后缀数组算法的应用

文章到这里，就是后缀算法的应用了。

先简单介绍一下能应用在什么问题之上。

最长公共前缀
单个字符串的相关问题
- 重复子串
- 字串的个数
- 回文子串
- 连续重复子串
两个字符串的相关问题
- 公共子串
- 字串的个数
多个字符串的相关问题

由于本人还没有做相关练习，这里先只介绍问题 1。其他的我先溜去做题了。

例 1：最长公共前缀

给定一个字符串，每次询问某两个后缀的最长公共前缀。

分析：

根据性质

$$ \text{lcp}(\text{suf}(j),\text{suf}(k))=\min\{\text{height}[\text{Rank}[j]+1],...,\text{height}[\text{Rank}[k]]\} $$

可以将问题转化成 RMQ 问题。如果用 ST 表，那么 $\text{O}(n\log n)$ 预处理， $\text{O}(1)$ 查询。

如果用 $\text{O}(n)$ 预处理 RMQ 问题，那么本题可以做到 $\text{O}(n)$。（虽然作者不会 $\text{O}(n)$ 预处理）

参考文献

[1] 罗穗骞，IOI2009 国家集训队论文《后缀数组——处理字符串的有力工具》
[2] OI-Wiki，《后缀数组简介》
[3] YxuanwKeith，《五分钟搞懂后缀数组！后缀数组解析以及应用(附详解代码)》

结尾

这篇笔记写得匆匆忙忙，昨天晚修开始写，写到今天早上。

有错误时不可避免的，欢迎读者指出我的错误。如有疑问或高见，也可以评论。

由于一上完课就来写笔记，还没做多少题目，这里只讲了最长公共前缀的算法分析，实在抱歉。

本人版权意识薄弱，如有侵权部分，请联系作者解决。

希望这篇笔记能帮到你，Thank you~